On October 24, 2024, the National Institute of Standards and Technology (NIST) announced that they’re advancing fourteen post-quantum signature schemes to the second round of the “signatures on ramp” competition. “Post-quantum” means that these algorithms are designed to resist the attack of quantum computers. NIST already standardized four post-quantum signature schemes (ML-DSA, SLH-DSA, XMSS, and LHS) and they are drafting a standard for a fifth (Falcon). Why do we need even more, you might ask? We’ll get to that.
A regular reader of the blog will know that this is not the first time we’ve taken measure of post-quantum signatures. In 2021 we took a first hard look, and reported on the performance impact we expect from large-scale measurements. Since then, dozens of new post-quantum algorithms have been proposed. Many of them have been submitted to this new NIST competition. We discussed some of the more promising ones in our early 2024 blog post.
In this blog post, we will go over the fourteen schemes advanced to the second round of the on ramp and discuss their feasibility for use in TLS — the protocol that secures browsing the Internet. The defining feature of practically all of them, is that they require much more bytes on the wire. Back in 2021 we shared experimental results on the impact of these extra bytes. Today, we will share some surprising statistics on how TLS is used in practice. One is that today already almost half the data sent over more than half the QUIC connections are just for the certificates.
For a broader context and introduction to the post-quantum migration, check out our early 2024 blog post. One take-away to mention here: there will be two migrations for TLS. First, we urgently need to migrate key agreement to post-quantum cryptography to protect against attackers that store encrypted communication today in order to decrypt it in the future when a quantum computer is available. The industry is making good progress here: 18% of human requests to websites using Cloudflare are secured using post-quantum key agreement. The second migration, to post-quantum signatures (certificates), is not as urgent: we will need to have this sorted by the time the quantum computer arrives. However, it will be a bigger challenge.
Before we have a look at the long list of post-quantum signature algorithms and their performance characteristics, let’s go through the signatures involved when browsing the Internet and their particular constraints.

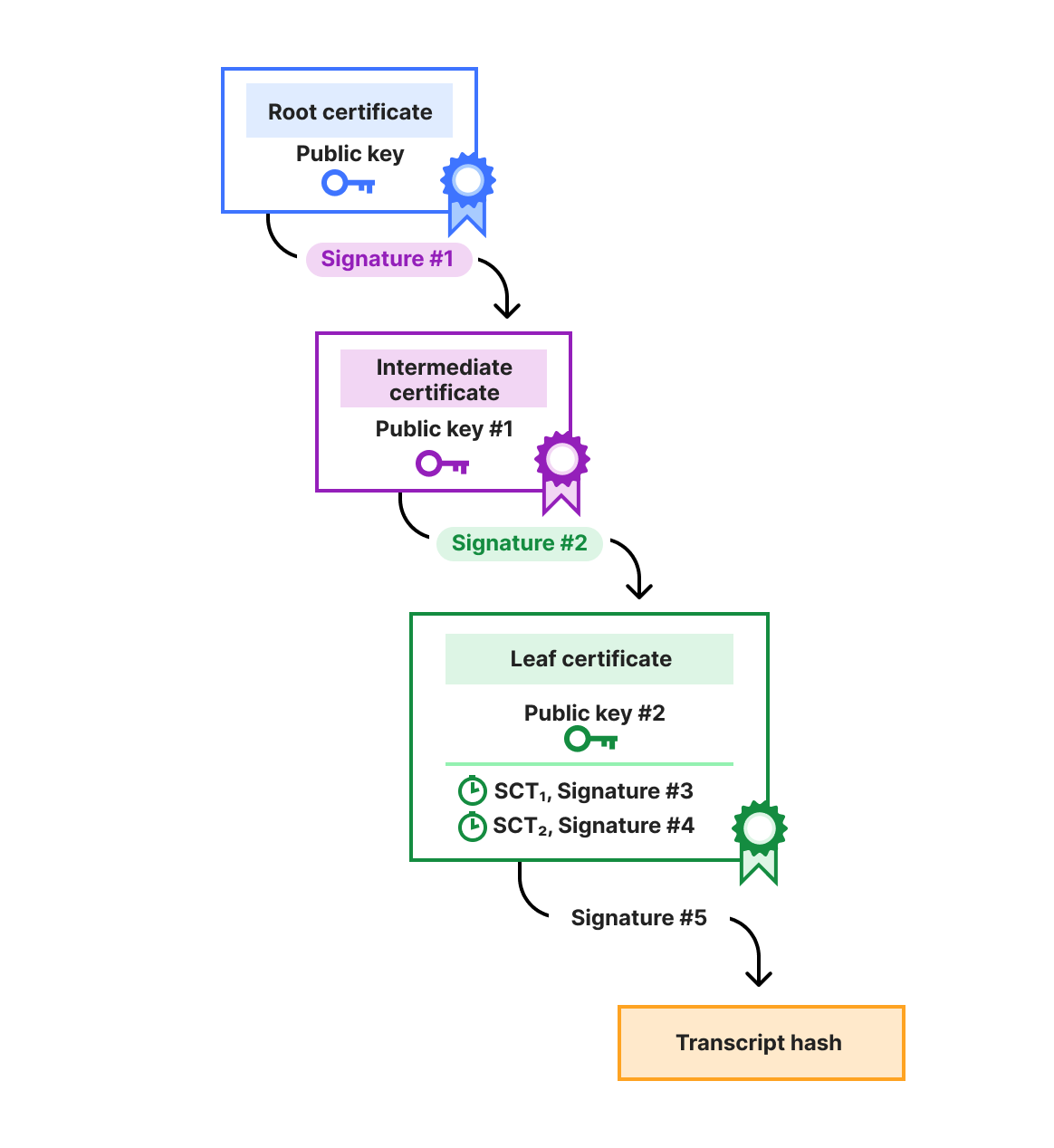
When you visit a website, the browser establishes a TLS connection with the server for that website. The connection starts with a cryptographic handshake. During this handshake, to authenticate the connection, the server signs the transcript so far, and presents the browser with a TLS leaf certificate to prove that it’s allowed to serve the website. This leaf certificate is signed by a certification authority (CA). Typically, it’s not signed by the CA’s root certificate, but by an intermediate CA certificate, which in turn is signed by the root CA, or another intermediate. That’s not all: a leaf certificate has to include at least two signed certificate timestamps (SCTs). These SCTs are signatures created by certificate transparency (CT) logs to attest they’ve been publicly logged. Certificate Transparency is what enables you to look up a certificate on websites such crt.sh and merklemap. In the future three or more SCTs might be required. Finally, servers may also send an OCSP staple to demonstrate a certificate hasn’t been revoked.
Thus, we’re looking at a minimum of five signatures (not counting the OCSP staple) and two public keys transmitted across the network to establish a new TLS connection.
Only the handshake transcript signature is created online; the other signatures are “offline”. That is, they are created ahead of time. For these offline signatures, fast verification is much more important than fast signing. On the other hand, for the handshake signature, we want to minimize the sum of signing and verification time.
Only the public keys of the leaf and intermediate certificates are transmitted on the wire during the handshake, and for those we want to minimize the combined size of the signature and the public key. For the other signatures, the public key is not transmitted during the handshake, and thus a scheme with larger public keys would be tolerable, and preferable if it trades larger public keys for smaller signatures.
Now that we’re up to speed, let’s have a look at the candidates that progressed (marked by 🤔 below), compared to the classical algorithms vulnerable to quantum attack (marked by ❌), and the post-quantum algorithms that are already standardized (✅) or soon will be (📝). Each submission proposes several variants. We list the most relevant variants to TLS from each submission. To explore all variants, check out Thom Wigger’s signatures zoo.
| Sizes (bytes) | CPU time (lower is better) | |||||
|---|---|---|---|---|---|---|
| Family | Name variant | Public key | Signature | Signing | Verification | |
| Elliptic curves | Ed25519 | ❌ | 32 | 64 | 0.15 | 1.3 |
| Factoring | RSA 2048 | ❌ | 272 | 256 | 80 | 0.4 |
| Lattices | ML-DSA 44 | ✅ | 1,312 | 2,420 | 1 (baseline) | 1 (baseline) |
| Symmetric | SLH-DSA 128s | ✅ | 32 | 7,856 | 14,000 | 40 |
| SLH-DSA 128f | ✅ | 32 | 17,088 | 720 | 110 | |
| LMS M4_H20_W8 | ✅ | 48 | 1,112 | 2.9 ⚠️ | 8.4 | |
| Lattices | Falcon 512 | 📝 | 897 | 666 | 3 ⚠️ | 0.7 |
| Codebased | CROSS R-SDP(G)1 small | 🤔 | 38 | 7,956 | 20 | 35 |
| LESS 1s | 🤔 | 97,484 | 5,120 | 620 | 1800 | |
| MPC in the head | Mirath Mirith Ia fast | 🤔 | 129 | 7,877 | 25 | 60 |
| MQOM L1-gf251-fast | 🤔 | 59 | 7,850 | 35 | 85 | |
| PERK I-fast5 | 🤔 | 240 | 8,030 | 20 | 40 | |
| RYDE 128F | 🤔 | 86 | 7,446 | 15 | 40 | |
| SDitH gf251-L1-hyp | 🤔 | 132 | 8,496 | 30 | 80 | |
| VOLE in the head | FAEST EM-128f | 🤔 | 32 | 5,696 | 6 | 18 |
| Lattices | HAWK 512 | 🤔 | 1,024 | 555 | 0.25 | 1.2 |
| Isogeny | SQISign I | 🤔 | 64 | 177 | 17,000 | 900 |
| Multivariate | MAYO one | 🤔 | 1,168 | 321 | 1.4 | 1.4 |
| MAYO two | 🤔 | 5,488 | 180 | 1.7 | 0.8 | |
| QR-UOV I-(31,165,60,3) | 🤔 | 23,657 | 157 | 75 | 125 | |
| SNOVA (24,5,4) | 🤔 | 1,016 | 248 | 0.9 | 1.4 | |
| SNOVA (25,8,3) | 🤔 | 2,320 | 165 | 0.9 | 1.8 | |
| SNOVA (37,17,2) | 🤔 | 9,842 | 106 | 1 | 1.2 | |
| UOV Is-pkc | 🤔 | 66,576 | 96 | 0.3 | 2.3 | |
| UOV Ip-pkc | 🤔 | 43,576 | 128 | 0.3 | 0.8 |
Some notes about the table. It compares selected variants of the submissions progressed to the second round of the NIST PQC signature on ramp with earlier existing traditional and post-quantum schemes at the security level of AES-128. CPU times are taken from the signatures zoo, which collected them from the submission documents and some later advances. CPU performance varies significantly by platform and implementation, and should only be taken as a rough indication. We are early in the competition, and the on-ramp schemes will evolve: some will improve drastically (both in compute and size), whereas others will regress to counter new attacks. Check out the zoo for the latest numbers. We marked Falcon signing with a ⚠️, as Falcon signing is hard to implement in a fast and timing side-channel secure manner. LMS signing has a ⚠️, as secure LMS signing requires keeping a state and the listed signing time assumes a 32MB cache. This will be discussed later on.
These are a lot of algorithms, and we didn’t even list all variants. One thing is clear: none of them perform as well as classical elliptic curve signatures across the board. Let’s start with NIST’s 2022 picks.
The most viable general purpose post-quantum signature scheme standardized today is the lattice-based ML-DSA (FIPS 204), which started its life as Dilithium. It’s light on the CPU and reasonably straightforward to implement. The big downside is that its signatures and public keys are large: 2.4kB and 1.3kB respectively. Here and for the balance of the blog post, we will only consider the variants at the AES-128 security level unless stated otherwise. Adding ML-DSA, adds 14.7kB to the TLS handshake (two 1312-byte public keys plus five 2420-byte signatures).
SLH-DSA (FIPS 205, née SPHINCS+) looks strictly worse, adding 39kB and significant computational overhead for both signing and verification. The advantage of SLH-DSA, being solely based on hashes, is that its security is much better understood than ML-DSA. The lowest security level of SLH-DSA is generally more trusted than the highest security levels of many other schemes.
Falcon (to be renamed FN-DSA) seems much better than SLH-DSA and ML-DSA if you look only at the numbers in the table. There is a catch though. For fast signing, Falcon requires fast floating-point arithmetic, which turns out to be difficult to implement securely. Signing can be performed securely with emulated floating-point arithmetic, but that makes it roughly twenty times slower. This makes Falcon ill-suited for online signatures. Furthermore, the signing procedure of Falcon is complicated to implement. On the other hand, Falcon verification is simple and doesn’t require floating-point arithmetic.
Leaning into Falcon’s strength, by using ML-DSA for the handshake signature, and Falcon for the rest, we’re only adding 7.3kB (at security level of AES-128).
There is one more difficulty with Falcon worth mentioning: it’s missing a middle security level. That means that if Falcon-512 (which we considered so far) turns out to be weaker than expected, then the next one up is Falcon-1024, which has double signature and public key size. That amounts to adding about 11kB.
The very first post-quantum signature algorithms standardized are the stateful hash-based XMSS(MT) and LMS/HSS. These are hash-based signatures, similar to SLH-DSA, and so we have a lot of trust in their security. They come with a big drawback: when creating a keypair you prepare a finite number of signature slots. For the variant listed in the table, there are about one million slots. Each slot can only be used once. If by accident a slot is used twice, then anyone can (probably) use those two signatures to forge any new signature from that slot and break into the connection the certificate is supposed to protect. Remembering which slots have been used, is the state in stateful hash-based signature. Certificate authorities might be able to keep the state, but for general use, Adam Langley calls keeping the state a huge foot-cannon.
There are more quirks to keep in mind for stateful hash-based signatures. To start, during key generation, each slot needs to be prepared. Preparing each slot takes approximately the same amount of time as verifying a signature. Preparing all million takes a couple of hours on a single core. For intermediate certificates of a popular certificate authority, a million slots are not enough. Indeed, Let’s Encrypt issues more than four million certificates per day. Instead of increasing the number of slots directly, we can use an extra intermediate. This is what XMSSMT and HSS do internally. A final quirk of stateful hash-based signatures is that their security is bottlenecked on non-repudiation: the listed LMS instance has 192 bits of security against forgery, but only 96 bits against the signer themselves creating a single signature that verifies two different messages.
Even when stateful hash-based signatures or Falcon can be used, we are still adding a lot of bytes on the wire. From earlier experiments we know that that will impact performance significantly. We summarize those findings later in this blog post, and share some new data. The short of it: it would be nice to have a post-quantum signature scheme that outperforms Falcon, or at least outperforms ML-DSA and is easier to deploy. This is one of the reasons NIST is running the second competition.
With that in mind, let’s have a look at the candidates.
With only performance in mind, it is surprising that half of the candidates do worse than ML-DSA. There is a good reason for it: NIST is worried that we’re putting all our eggs in the structured lattices basket. SLH-DSA is an alternative to lattices today, but it doesn’t perform well enough for many applications. As such, NIST would primarily like to standardize another general purpose signature algorithm that is not based on structured lattices, and that outperforms SLH-DSA. We will briefly touch upon these schemes here.
Code-based
CROSS and LESS are two code-based signature schemes. CROSS is based on a variant of the traditional syndrome decoding problem. Its signatures are about as large as SLH-DSA, but its edge over SLH-DSA is the much better signing times. LESS is based on the novel linear equivalence problem. It only outperforms SLH-DSA on signature size, requiring larger public keys in return. For use in TLS, the high verification times of LESS are especially problematic. Given that LESS is based on a new approach, it will be interesting to see how much it can improve going forward.
Multi-party computation in the head
Five of the submissions (Mirath, MQOM, PERK, RYDE, SDitH) use the Multi-Party Computation in the Head (MPCitH) paradigm.
It has been exciting to see the developments in this field. To explain a bit about it, let’s go back to Picnic. Picnic was an MPCitH submission to the previous NIST PQC competition. In essence, its private key is a random key x, and its public key is the hash H(x). A signature is a zero-knowledge proof demonstrating that the signer knows x. So far, it’s pretty similar in shape to other signature schemes that use zero knowledge proofs. The difference is in how that proof is created. We have to talk about multi-party computation (MPC) first. MPC starts with splitting the key x into shares, using Shamir secret sharing for instance, and giving each party one share. No single party knows the value of x itself, but they can recover it by recombining. The insight of MPC is that these parties (with some communication) can perform arbitrary computation on the data they shared. In particular, they can compute a secret share of H(x). Now, we can use that to make a zero-knowledge proof as follows. The signer simulates all parties in the multi-party protocol to compute and recombine H(x). The signer then reveals part of the intermediate values of the computation using Fiat–Shamir: enough so that none of the parties could have cheated on any of the steps, but not enough that it allows the verifier to figure out x themselves.
For H, Picnic uses LowMC, a block cipher for which it’s easy to do the multi-party computation. The initial submission of Picnic performed poorly compared to SLH-DSA with 32kB signatures. For the second round, Picnic was improved considerably, boasting 12kB signatures. SLH-DSA won out with smaller signatures, and more conservative security assumptions: Picnic relies on LowMC which didn’t receive as much study as the hashes on which SLH-DSA is based.
Back to the MPCitH candidates that progressed. All of them have variants (listed in the table) with similar or better signature sizes as SLH-DSA, while outperforming SLH-DSA considerably in signing time. There are variants with even smaller signatures, but their verification performance is significantly higher. The difference between the MPCitH candidates is the underlying trapdoor they use. In Picnic the trapdoor was LowMC. For both RYDE and SDiTH, the trapdoors used are based on variants of syndrome decoding, and could be classified as code-based cryptography.
Over the years, MPCitH schemes have seen remarkable improvements in performance, and we don’t seem to have reached the end of it yet. There is still some way to go before these schemes would be competitive in TLS: signature size needs to be reduced without sacrificing the currently borderline acceptable verification performance. On top of that, not all underlying trapdoors of the various schemes have seen enough scrutiny.
FAEST
FAEST is a peek into the future. It’s similar to the MPCitH candidates in that its security reduces to an underlying trapdoor. It is quite different from those in that FAEST’s underlying trapdoor is AES. That means that, given the security analysis of FAEST is correct, it’s on the same footing as SLH-DSA. Despite the conservative trapdoor, FAEST beats the MPCitH candidates in performance. It also beats SLH-DSA on all metrics.
At the AES-128 security level, FAEST’s signatures are larger than ML-DSA. For those that want to hedge against improvements in lattice attacks, and would only consider higher security levels of ML-DSA, FAEST becomes an attractive alternative. ML-DSA-65 has a combined public key and signature size of 5.2kB, which is similar to FAEST EM-128f. ML-DSA-65 still has a slight edge in performance.
FAEST is based on the 2023 VOLE in the Head paradigm. These are new ideas, and it seems likely their full potential has not been realized yet. It is likely that FAEST will see improvements.
The VOLE in the Head techniques can and probably will be adopted by some of the MPCitH submissions. It will be interesting to see how far VOLEitH can be pushed when applied to less conservative trapdoors. Surpassing ML-DSA seems in reach, but Falcon? We will see.
Now, let’s move on to the submissions that surpass ML-DSA today.
HAWK is similar to Falcon, but improves upon it in a few key ways. Most importantly, it doesn’t rely on floating point arithmetic. Furthermore, its signing procedure is simpler and much faster. This makes HAWK suitable for online signatures. Using HAWK adds 4.8kB. Apart from size and speed, it’s beneficial to rely on only a single scheme: using multiple schemes increases the attack surface for algorithmic weaknesses and implementation mistakes.
Similar to Falcon, HAWK is missing a middle security level. Using HAWK-1024 doubles sizes (9.6kB).
There is one downside to HAWK over Falcon: HAWK relies on a new security assumption, the lattice isomorphism problem.
SQISign is based on isogenies. Famously, SIKE, another isogeny-based scheme in the previous competition, got broken badly late into the competition. SQISign is based on a different problem, though. SQISign is remarkable for having very small signatures and public keys: it even beats RSA-2048. The glaring downside is that it is computationally very expensive to compute and verify a signature. Isogeny-based signature schemes is a very active area of research with many advances over the years.
It seems unlikely that any future SQISign variant will sign fast enough for the TLS handshake signature. Furthermore, SQISign signing seems to be hard to implement in a timing side-channel secure manner. What about the other signatures of TLS? The bottleneck is verification time. It would be acceptable for SQISign to have larger signatures, if that allows it to have faster verification time.
UOV (unbalanced oil and vinegar) is an old multivariate scheme with large public keys (67kB), but small signatures (96 bytes). Furthermore, it has excellent signing and verification performance. These interesting size tradeoffs make it quite suited for use cases where the public key is known in advance.
If we use UOV in TLS for the SCTs and root CA, whose public keys are not transmitted when setting up the connection, together with ML-DSA for the others, we’re looking at 7.2kB. That’s a clear improvement over using ML-DSA everywhere, and a tad better than combining ML-DSA with Falcon.
When combining UOV with HAWK instead of ML-DSA, we’re looking at adding only 3.4kB. That’s better again, but only a marginal improvement over using HAWK everywhere (4.8kB). The relative advantage of UOV improves if the certificate transparency ecosystem moves towards requiring more SCTs.
For SCTs, the size of UOV public keys seems acceptable, as there are not that many certificate transparency logs at the moment. Shipping a UOV public key for hundreds of root CAs is more painful, but within reason. Even with intermediate suppression, using UOV in each of the thousands of intermediate certificates does not make sense.
Since the original UOV, over the decades, many attempts have been made to add additional structure UOV, to get a better balance between the size of the signature and public key. Unfortunately many of these structured multivariate schemes, which include GeMMS and Rainbow, have been broken.
Let’s have a look at the multivariate candidates. The most interesting variant of QR-UOV for TLS has 24kB public keys and 157 byte signatures. The current verification times are unacceptably high, but there seems to be plenty of room for an improved implementation. There is also a variant with a 12kB public key, but its verification time needs to come down even further. In any case, the combined size QR-UOV’s public key and signatures remain large enough that it’s not a competitor of ML-DSA or Falcon. Instead, QR-UOV competes with UOV, where UOV’s public keys are unwieldy. Although QR-UOV hasn’t seen a direct attack yet, a similar scheme has recently been weakened and another broken.
Finally, we get to SNOVA and MAYO. Although they’re based on a different technique, they have a lot of properties in common. To start, they have the useful property that they allow for a granular tradeoff between public key and signature size. This allows us to use a different variant optimized for whether we’re transmitting the public in the connection or not. Using MAYOone for the leaf and intermediate, and MAYOtwo for the others, adds 3.5kB. Similarly with SNOVA, we add 2.8kB. On top of that, both schemes have excellent signing and verification performance.
The elephant in the room is the security. During the end of the first round, a new generic attack on underdefined multivariate systems prompted the MAYO team to tweak their parameters slightly. SNOVA has been hit a bit harder by three attacks (1, 2, 3), but so far it seems that SNOVA’s parameters can be adjusted to compensate.
Ok, we had a look at all the candidates. What did we learn? There are some very promising algorithms that will reduce the number of bytes required on the wire compared to ML-DSA and Falcon. None of the practical ones will prevent us from adding any extra bytes to TLS. So, given that we must add some bytes: how many extra bytes are too many?
On average, around 15 million TLS connections are established with Cloudflare per second. Upgrading each to ML-DSA, would take 1.8Tbps, which is 0.6% of our current total network capacity. No problem so far. The question is how these extra bytes affect performance.
Back in 2021, we ran a large-scale experiment to measure the impact of big post-quantum certificate chains on connections to Cloudflare’s network over the open Internet. There were two important results. First, we saw a steep increase in the rate of client and middlebox failures when we added more than 10kB to existing certificate chains. Secondly, when adding less than 9kB, the slowdown in TLS handshake time would be approximately 15%. We felt the latter is workable, but far from ideal: such a slowdown is noticeable and people might hold off deploying post-quantum certificates before it’s too late.
Chrome is more cautious and set 10% as their target for maximum TLS handshake time regression. They report that deploying post-quantum key agreement has already incurred a 4% slowdown in TLS handshake time, for the extra 1.1kB from server-to-client and 1.2kB from client-to-server. That slowdown is proportionally larger than the 15% we found for 9kB, but that could be explained by slower upload speeds than download speeds.
There has been pushback against the focus on TLS handshake times. One argument is that session resumption alleviates the need for sending the certificates again. A second argument is that the data required to visit a typical website dwarfs the additional bytes for post-quantum certificates. One example is this 2024 publication, where Amazon researchers have simulated the impact of large post-quantum certificates on data-heavy TLS connections. They argue that typical connections transfer multiple requests and hundreds of kilobytes, and for those the TLS handshake slowdown disappears in the margin.
Are session resumption and hundreds of kilobytes over a connection typical though? We’d like to share what we see. We focus on QUIC connections, which are likely initiated by browsers or browser-like clients. Of all QUIC connections with Cloudflare that carry at least one HTTP request, 37% are resumptions, meaning that key material from a previous TLS connection is reused, avoiding the need to transmit certificates. The median number of bytes transferred from server-to-client over a resumed QUIC connection is 4.4kB, while the average is 395kB. For non-resumptions the median is 7.8kB and average is 551kB. This vast difference between median and average indicates that a small fraction of data-heavy connections skew the average. In fact, only 15.8% of all QUIC connections transfer more than 100kB.
The median certificate chain today (with compression) is 3.2kB. That means that almost 40% of all data transferred from server to client on more than half of the non-resumed QUIC connections are just for the certificates, and this only gets worse with post-quantum algorithms. For the majority of QUIC connections, using ML-DSA as a drop-in replacement for classical signatures would more than double the number of transmitted bytes over the lifetime of the connection.
It sounds quite bad if the vast majority of data transferred for a typical connection is just for the post-quantum certificates. It’s still only a proxy for what is actually important: the effect on metrics relevant to the end-user, such as the browsing experience (e.g. largest contentful paint) and the amount of data those certificates take from a user’s monthly data cap. We will continue to investigate and get a better understanding of the impact.
That was a lot — let’s step back.
It’s great to see how much better the post-quantum signature algorithms are today in almost every family than they were in 2021. The improvements haven’t slowed down either. Many of the algorithms that do not improve over ML-DSA for TLS today could still do so in the third round. Looking back, we are also cautioned: several algorithms considered in 2021 have since been broken.
From an implementation and performance perspective for TLS today, HAWK, SNOVA, and MAYO are all clear improvements over ML-DSA and Falcon. They are also very new, and presently we cannot depend on them without a plan B. UOV has been around a lot longer. Due to its large public key, it will not work on its own, but be a very useful complement to another general purpose signature scheme.
Even with the best performers out of the competition, the way we see TLS connections used today, suggest that drop-in post-quantum certificates will have a big impact on at least half of them.
In the meantime, we can also make plan B our plan A: there are several ways in which we can reduce the number of signatures used in TLS. We can leave out intermediate certificates (1, 2, 3). Another is to use a KEM instead of a signature for handshake authentication. We can even get rid of all the offline signatures with a more ambitious redesign for the vast majority of visits: a post-quantum Internet with fewer bytes on the wire! We’ve discussed these ideas at more length in a previous blog post.
So what does this mean for the coming years? We will continue to work with browsers to understand the end user impact of large drop-in post-quantum certificates. When certificate authorities support them (our guess: 2026), we will add support for ML-DSA certificates for free. This will be opt-in until cryptographically relevant quantum computers are imminent, to prevent undue performance regression. In the meantime, we will continue to pursue larger changes to the WebPKI, so that we can bring full post-quantum security to the Internet without performance compromise.
We’ve talked a lot about certificates, but what we need to care about today is encryption. Along with many across industry, including the major browsers, we have deployed the post-quantum key agreement X25519MLKEM768 across the board, and you can make sure your connections with Cloudflare are already secured against harvest-now/decrypt-later. Visit pq.cloudflareresearch.com to learn how.